
De driehoek van Pascal[1] is een rangschikking van de binomiaalcoëfficiënten in rijen voor toenemende beginnend met en op elke rij de binomiaalcoëfficiënten voor de mogelijke waarden van , lopend van tot en met . In de driehoek komt de eigenschap tot uitdrukking dat elke binomiaalcoëfficiënt de som is van de twee bovenliggende. De driehoek is naar de Franse wiskundige Blaise Pascal (1623 - 1662) genoemd, die de eerste Europeaan was die ermee rekende.
Het element in rij op de positie is dus:
- ,
voor en . De elementen kunnen recursief worden gedefinieerd door:
en
De getallen in de driehoek geven het aantal wegen aan vanaf de top naar de plaats van zo'n getal, waarmee ook de besproken eigenschap verklaard is. Omdat er steeds 2 keuzen zijn om de weg naar onder te vervolgen is de som van de getallen op een rij de overeenkomstige een macht van 2.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 1 10 45 120 210 252 210 120 45 10 1 Eerste 11 rijen
Pascal ordende de getallen van de driehoek overigens in een rechthoekig schema:
1 1 1 1 1 1 1 1 1 1 1 1 2 3 4 5 6 7 8 9 10 1 3 6 10 15 21 28 36 45 1 4 10 20 35 56 84 120 1 5 15 35 70 126 210 1 6 21 56 126 252 1 7 28 84 210 1 8 36 120 1 9 45 1 10 1
en noemde het getal op het kruispunt van rij en kolom , zodat
en de genoemde eigenschap luidt:
Geschiedenis

De vroegste gedetailleerde beschrijving van een driehoek van binomiaalcoëfficiënten verscheen in de 10de eeuw in commentaren op Chandas Shastra, een Indiaas boek over de prosodie van Sanskriet, geschreven door Pingala tussen de vijfde en tweede eeuw v.Chr. Hoewel Pingala's werk alleen in fragmenten bewaard is gebleven, gebruikte de commentator Halayudha de driehoek rond 975 om twijfelachtige relaties te leggen met de Meru-prastaara, de trappen van de mythologische berg Meru. Het was ook al bekend dat de som van de vlakke diagonalen van de driehoek de rij van Fibonacci oplevert. Door de Indiase wiskundige Bhattotpala rond 1068 zijn de eerste 17 regels van de driehoek overgeleverd.
Ongeveer in dezelfde tijd werd de driehoek van Pascal in Perzië behandeld door al-Karaji (953-1029) en Omar Khayyám, en is daarom in het tegenwoordige Iran bekend als de driehoek van Khayyám. Men kende verscheidene wiskundige uitspraken over de driehoek, waaronder het binomium van Newton. Het is vrij zeker dat Khayyām een methode gebruikte om de -de-machtswortel te berekenen die berust op de binomiale ontwikkeling, dus op de binomiaalcoëfficiënten.
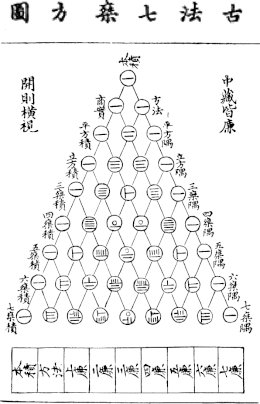
De vroegste Chinese voorstelling van een meetkundige figuur, overeenkomend met de driehoek van Pascal staat in het boek van Yang Hui Xiangjie Jiuzhang suanfa uit 1261, waarvan fragmenten in de Yongle dadian bewaard zijn gebleven, een encyclopedie die tussen 1403 en 1408 is samengesteld. [2] Yang schrijft daarin de driehoek van Jia Xian, omstreeks 1050, overgenomen te hebben, als ook li cheng shi shuo, 'bepaling coëfficiënten door middel van een schema', een methode voor het berekenen van vierkants- en derdemachtswortels.[3][4]
Peter Apian publiceerde de driehoek in 1531-1532 op de omslag van zijn boek over handelsberekeningen, waarvan in een eerdere versie uit 1527 de driehoek van Pascal voor het eerst in de literatuur in Europa wordt genoemd.
Blaise Pascal publiceerde in 1655 het boek Traité du triangle arithmétique, 'Verhandeling over de meetkundige driehoek', waarin hij verscheidene resultaten met betrekking tot de driehoek bijeenbracht en die gebruikte om problemen in de kansrekening op te lossen, in het bijzonder bij het dobbelen en bij het oplossen van het puntenprobleem, het probleem van de afgebroken partij. De driehoek werd later door Pierre Rémond de Montmort (1708) en Abraham de Moivre (1730) naar Pascal genoemd. Pascal noemde zijn ontdekking de géometrie du hasard, de meetkunde van het toeval. De getallendriehoek was veel eerder bekend, maar de toepassing ervan in de kansrekening was Pascals ontdekking.
Eigenschappen

- De som van de binomiaalcoëficiënten in rij is gelijk aan
- De getallen op een rij vormen de coëfficiënten van het binomium van Newton
- Als de binomiaalcoëfficiënt in de rij met index een priemgetal is, zijn alle coëfficiënten in die rij, behalve de 1 aan het begin en eind, delers van l. Voorbeeld: 1 7 21 35 35 21 7 1
- Door de oneven getallen in de driehoek weer te geven als een zwarte punt ontstaat een figuur met een fractale structuur, de driehoek van Sierpiński.
- De rij getallen evenwijdig aan een van de zijden van de driehoek heet een diagonaal. De eerste diagonaal bevat alleen getallen 1. De tweede diagonaal de natuurlijke getallen. De getallen op de derde diagonaal zijn de driehoeksgetallen. Deze zijn gelijk aan
- Op de vierde diagonaal staan de tetraëdergetallen.
- De getallen uit de rij van Fibonacci verschijnen ook in de driehoek als som van een ander soort diagonalen.
- Het bord van Galton of quincunx lijkt op de driehoek van Pascal, is door de Britse bioloog, wis- en natuurkundige Francis Galton (1822–1911) ontworpen en wordt ervoor gebruikt om te demonstreren hoe de binomiale verdeling ontstaat.
- ↑ rij A007318 in OEIS
- ↑ Ho Peng Yoke Li, Qi en Shu (1985). An Introduction to Science and Civilization in China. Hongkong University Press, pp. 97. ISBN 0-486-41445-0.
- ↑ George Gheverghese Joseph (2011). The Crest of the Peacock. Non-European Roots of Mathematics, 3. Princeton University Press, 247. ISBN 978-0-691-13526-7.
- ↑ Duan Yao-Yung, Kostas Nikolantonakis (2011). The Algorithm of Extraction in Greek and Sino-Indian Mathematical Traditions.. Birkhäuser. DOI:10.1007/978-0-8176-4695-0_11, 180–181. ISBN 978-0-8176-4695-0.





























