Chemische binding
Dipool-dipoolinteractie
Moleculen (intramoleculair)
Covalente binding
Moleculen (intermoleculair)
Vanderwaalskrachten Waterstofbrug
Zouten
Ionbinding Ion-dipoolkrachten
Metalen
Metaalbinding
Covalente netwerken
Covalente binding
Theorieën
Lewistheorie Valentiebindingstheorie VSEPR-theorie Molecuulorbitaaltheorie
Eigenschappen
Bindingslengte Bindingshoek Bindingsenthalpie Bindingsenergie Bindingsorde Elektronegativiteit Roosterenthalpie
Portaal    Scheikunde

De valentieschil-elektronenpaar-repulsie-theorie (meestal benoemd als VSEPR-theorie) is een theorie die de geometrie van covalente bindingen verklaart aan de hand van Paulirepulsie tussen valentie-elektronen. De theorie gaat ervan uit dat de atomen in een molecuul zich rond één centraal atoom bevinden en wel zodanig dat hun onderlinge afstand zo groot mogelijk is. Verder wordt aangenomen dat dit ook geldt voor vrije elektronparen.

Het sterisch getal is de som van het aantal bindingpartners en het aantal vrije elektronenparen. Dit getal varieert van 2 tot 6. Onderstaande tabel geeft een overzicht van sterische getallen van enkele verbindingen:

Alle elektronenparen in een molecuul oefenen repulsieve coulombkrachten op elkaar uit. Als gevolg hiervan oriënteren alle elektronenparen zich zodanig op een denkbeeldig boloppervlak, dat hun onderlinge afstand maximaal is. Daardoor krijgen alle covalente bindingen met eenzelfde sterisch getal steeds 1 unieke moleculair-geometrische basisconfiguratie:

• 2: lineair
• 3: trigonaal planair
• 4: tetraëdrisch
• 5: trigonaal bipiramidaal
• 6: octaëdrisch

Zie Moleculaire geometrie en AXE-methode voor de hoofdartikelen over dit onderwerp.

De werkelijke geometrie komt niet steeds overeen met de basisconfiguraties. Niet zelden bezitten elementen één of meerdere vrije elektronenparen. Deze werken de repulsieve interacties nog sterker in de hand. Desgevolgend ontstaan er veel meer mogelijkheden, afhankelijk van het aantal vrije elektronenparen. Onderstaande tabel geeft een overzicht van de meest voorkomende moleculaire geometrieën:

AXE-symbool	B. p.	V. p.	Moleculaire geometrie	Hoek(en)	Voorbeeld	Structuur
AX2E0	2	0	lineair	180°	BeCl2
AX3E0	3	0	trigonaal planair	120°	BF3
AX2E1	2	1	geknikt	< 120°	SO2
AX4E0	4	0	tetraëder	109,5°	CH4
AX3E1	3	1	trigonale piramide	107° < 109,5˚	NH3
AX2E2	2	2	gebogen	105˚< 109,5˚	H2O
AX5E0	5	0	trigonale bipiramide	90°, 120°	PCl5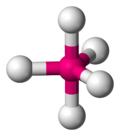
AX4E1	4	1	seesaw	90°, 120°, 180°	SF4
AX3E2	3	2	T-vormig	90°, 180°	ClF3
AX2E3	2	3	lineair	180°	XeF2
AX6E0	6	0	octaëder	90°	SF6
AX5E1	5	1	vierkante piramide	90°	BrF5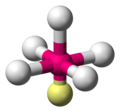
AX4E2	4	2	vierkant planair	90°	PtCl4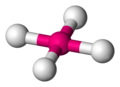
AX5E2	5	2	pentagonaal planair	72°	XeF5-
AX6E1	6	1	pentagonale piramide	90°, 72°	IOF52−
AX7E0	7	0	pentagonale bipiramide	90°, 72°	IF7